Introduction
The world surrounding us is made of atomic nuclei and nuclear matter. In this project, we investigate such strongly interacting systems under extreme conditions, given by large pressures and densities as they are found in neutron stars and along the edges of the three-dimensional hypernuclear chart, where there is a strong competition between attractive and repulsive forces, requiring high-precision calculations to understand the emergence of the drip lines when protons, neutrons or hyperons are added to a given atomic nucleus.
| Principal investigator: | Prof. Dr. Dr. h.c. Ulf-G. Meißner |
| Project manager: | Dr. Fabian Hildenbrand |
| Researchers: | Prof. Dr. Serdar Elhatisari, Dr. Shuang Zhang, Dr. Hui Tong, MSc. Helen Meyer, |
| Date published: | February 2025 |
| HPC platform used: | HoreKa |
| Institute: | HISKP IAS-4 |
| Affiliation: | Universität Bonn Forschungszentrum Jülich |
| Research field: | Physics |
| Project ID: | 23290 |
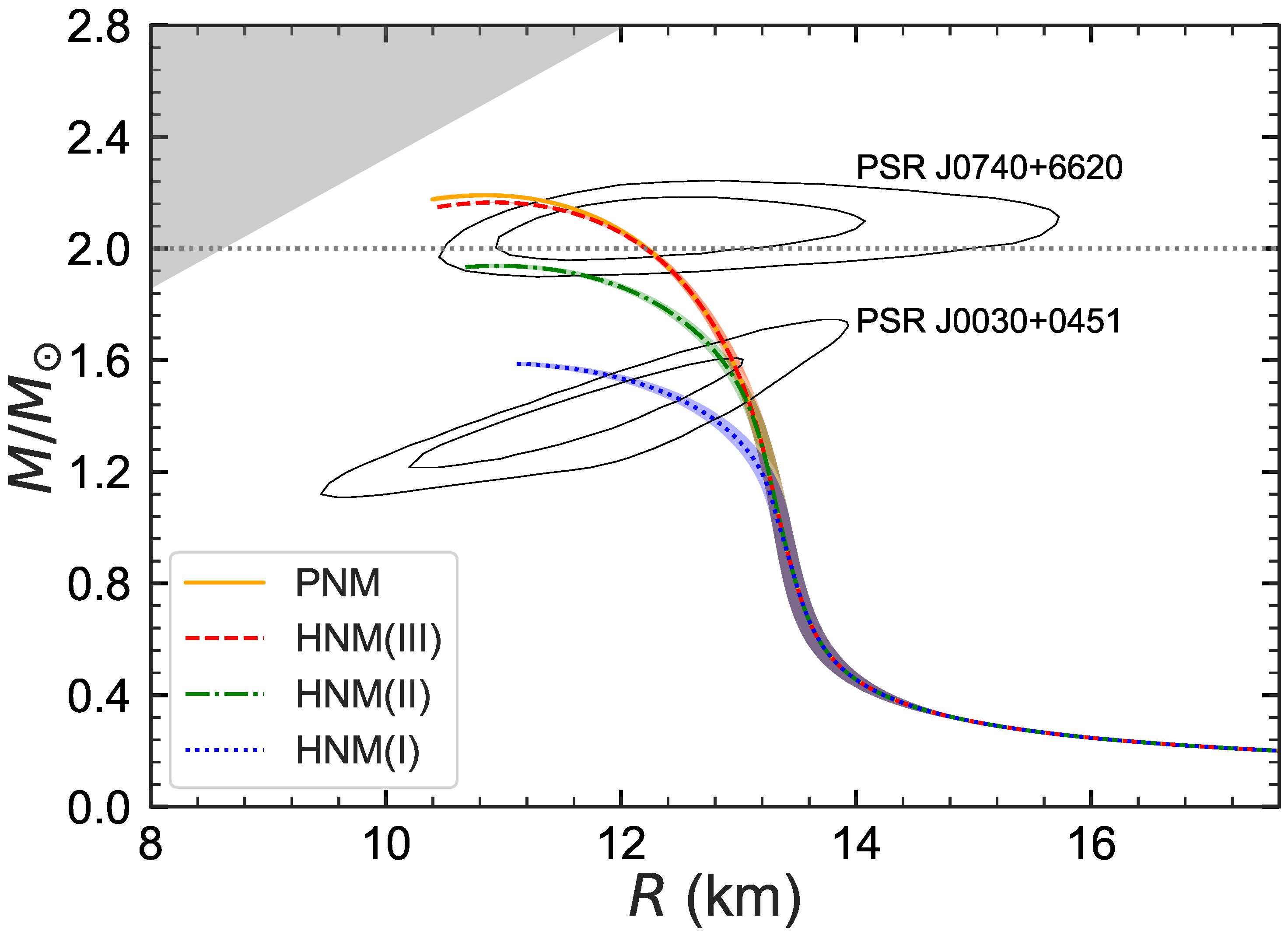
Figure: Neutron star mass-radius relation for various ab initio neutron matter equations of state. PNM refers to pure neutron matter, whereas HNM(I), HNM(II) and HNM(III) correspond to different ways of including Lambda hyperons. The gray horizontal dotted line represents twice the solar mass. The inner and outer contours indicate the allowed area of mass and radius of neutron stars by NICER’s analysis of PSR J0030+0451 [8] and PSR J0740+6620 [9]. The excluded causality region is also shown by the grey shaded region [10].
Project description
The matter we are made of is composed of atomic nuclei, which are held together by the strong force overcoming the repulsive Coulomb interaction between protons. A big questions is: How many protons or neutrons can one add to a given nucleus until no more bound many-body systems are generated? Another interesting question is related to the appearance of strange quarks in atomic nuclei, manifested by a number of hyperons bound to the core of protons and neutrons. What are the properties of such systems and how many of these exist? Another manifestation of the strong force is more macroscopic, as a large number of neutrons can form neutron stars, objects with up to two times the solar mass and radii in the range from 10 to 15 km. If one adds hyperons to such systems, the equation of state (EoS) is softened, decreasing the possible maximum mass of neutron stars below the observed bounds. This so-called hyperon-puzzle is one of the big challenges in nuclear astrophysics. All these questions can be addressed in the framework of Nuclear Lattice Effective Field Theory (NLEFT) that combines the chiral effective field theory for nuclear forces advocated by Nobel Laureate Steven Weinberg [1] with stochastic Monte Carlo (MC) methods to exactly solve the nuclear A-body problem [2]. This method has been very successful already in solving problems that could not be solved with existing methods, like ab initio calculations of the famous Hoyle state in 12C, that is responsible for generating sufficient amounts of carbon and oxygen in stars, or the first ever calculation of alpha-alpha scattering, which was impossible using the well-established conventional methods [3,4].
A major hurdle in this type of MC simulations is the so-called sign problem, that seems to make precision calculations impossible. Here, the nuclear forces are priviliged, as they feature an approcimate spin-isopsin SU(4) symmetry, which largely suppresses sign oscillations. However, to overcome the remaining sign oscillations, the new method of wavefunction matching (WFM) was invented. Wavefunction matching transforms the interaction between particles so that the wavefunctions up to some finite range match that of an easily computable interaction. This allows for calculations of systems that would otherwise be impossible due the MC sign cancellations. We applied the method already to lattice MC simulations of light nuclei, medium-mass nuclei, neutron matter, and nuclear matter, using high-fidelity chiral effective field theory interactions at N3LO, finding good agreement with empirical data [5]. Another important breakthrough was the fromulation of an auxiliary field formalism, that allowed for the first time for simulations with more than 220 neutrons and 110 Lambda hyperons in a finite volume, corresponding to densities of about six times the density of nuclear matter, thus enabling the calculation of neutron star properties from first principles [6]. In addition, we already explored the hypernuclear chart up to the oxygen region [7], which was also a major step in this field.
Based on these achievements, we want to address the following issues in this project:
- The radii and density profiles of proton-rich nuclei;
- The exploration of the hypernuclear chart with high-fidelity baryon-baryon interactions;
- The properties of proton-rich hypernuclear matter and the hyperon puzzle.
References
[1] S. Weinberg, Phys. Lett. B 251 (1990) 288-292.
[2] T.A. Lähde and Ulf-G. Meißner, Lect. Notes Phys. 957 (2019) 1-396.
[3] E.Epelbaum, H. Krebs, D. Lee and Ulf-G. Meißner, Phys. Rev. Lett. 106 (2011) 192501.
[4] S. Elhatisari et al., Nature 528 (2015) 111.
[5] S. Elhatisari et al., Nature 630 (2024) 59-63.
[6] H. Tong, S. Elhatisari and Ulf-G. Meißner, Sci. Bull. (2025) in print, https://doi.org/10.1016/j.scib.2025.01.008.
[7] F. Hildenbrand, S. Elhatisari, Z. Ren and Ulf-G. Meißner, Eur. Phys. J. A 60 (2024) 215.
[8] M.C. Miller et al., Astrophys. J. Lett. 887 (2019) L24.
[9] T.E. Riley et al., Astrophys. J. Lett. 918 (2019) L27.
[10] J.M. Lattimer and M. Prakash, Phys. Rept. 442 (2007) 109-165.